Qu'est ce que le nombre d'or?

Le nombre d’or fait appel à la perfection, la beauté. Qu’est-ce que c’est que le nombre d’or du point de vue de la géométrie sacrée ? Les détails ici.

Design, art, architecture, nature, philosophie, mathématiques… On retrouve le nombre d’or partout et autour de nous. Il se cache dans toutes les grandes œuvres de ce monde. Il captive les artistes pour ses propriétés. Le nombre d’or représenterait le rapport et la convenance, c’est-à-dire « la proportion divine ».

Noté en phi pour rendre hommage au sculpteur grec Phidias, né au Vème siècle av. J.-C., pour sa grande contribution à la décoration du Parthénon sur l’Acropole à Athènes, le nombre d’or est la dimension idéale. A l’œil humain, il allie l’équilibre à l’agréable. C’est la proportion parfaite. Mais à quoi sert le nombre d’or de façon globale et plus précisément dans la géométrie sacrée ? La réponse dans cet article.

Le nombre d’or : qu’est-ce que c’est ?

Avant tout, le nombre d’or est la représentation de la lettre φ issue de l' alphabet grec, et qui se prononce « Phi » en mathématiques. C’est un nombre irrationnel : 1,6180339887… Il ne s’écrit pas sous la forme d’une fraction dans laquelle a et b sont deux entiers relatifs.

En effet, le nombre d’or résulte de la division de deux longueurs, c’est donc une dimension, qu’on nomme la proportion d’or ou la « divine proportion » en géométrie. On dit donc que la dimension ou la proportion est d’or lorsque le lien ou le rapport entre la petite et la grande partie est semblable ou égal au lien entre le grand rapport et tout.

Aussi bien en mathématiques qu’en géométrie, le nombre d’or dispose des propriétés qui suscitent une profonde attirance. Par excellence, ce nombre se retrouve dans la nature. De même, on le retrouve dans d’autres domaines à savoir:

• L’arithmétique ;
• La suite de Fibonacci ;
• La géométrie ;
• Le rectangle d’or ;
• Le Triangle d’or ;
• L’angle d’or ;
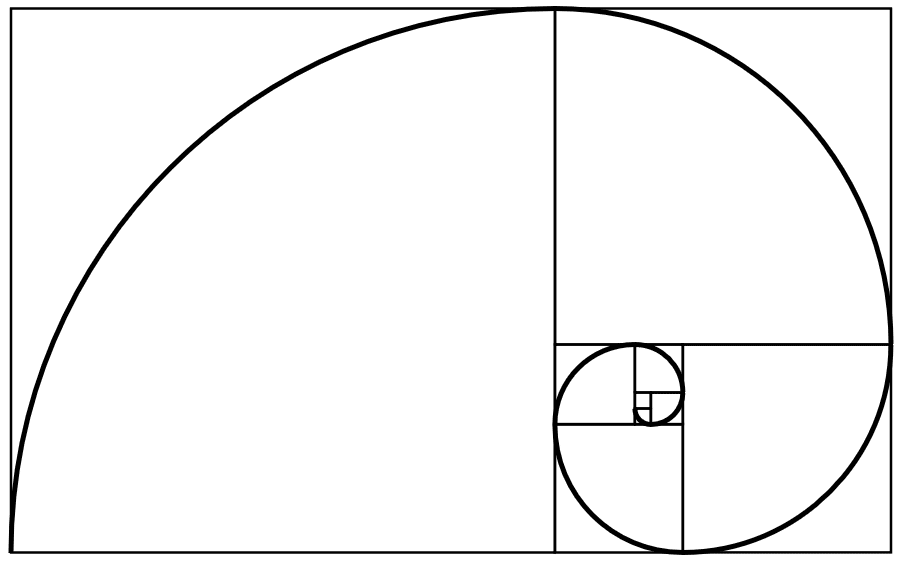
• La spirale d’or ;
• Le pentagone régulier ;
• La phyllotaxie ;
• L’art ;
• La peinture ;
• L’architecture ;
• Le design.

Nombre d’or : historique et proportions divines

Il est difficile à dater dans l’antiquité la connaissance et l’utilisation du nombre d’or à cause de l’absence de documents parlant du sujet à cette époque. D’aucuns pensent et avancent même que la pyramide de Khéops (vers 2600 av. J.-C.) pourrait contenir une proportion se calculant à l’aide du nombre d’or. Pour d’autres encore, les disciples de Pythagore et ceux qui suivaient la propriété de Pythagore auraient également étudié et connu le nombre d’or. Mais ils n’auraient laissé ni de trace écrite ni d’histoire orale.

Vers 300 av. J.-C. le mathématicien grec Euclide évoquait déjà dans ses ouvrages la proportion d’or. Cependant, Platon est à l’origine de l’étude de cette section dorée comme objet d’étude à part entière. Cette proportion n’avait pas encore l’appellation du nombre d’or à cette époque.

Le nombre d’or au Moyen-âge

Grâce à ses recherches, le mathématicien Al-Khawarizmi apporte une nouvelle façon de voir la proportion dorée. Il a proposé de nombreux problèmes consistant à diviser une longueur de dix unités en deux parties. La taille initiale divisée par le nombre d’or est la solution trouvée de l’un d’eux.

Leonardo Fibonacci est allé plus loin dans ses recherches et a pu découvrir la suite de Fibonacci en 1200. A cette époque, sa découverte ne se rapprochait pas encore du nombre d’or. C’est en 1260 que Campanus parvient à démontrer l’irrationalité du nombre d’or à travers la descente infinie qu’on peut voir dans la spirale d’or. 

L’époque de la Renaissance et le nombre d’or

Dans son livre intitulé De divina proportione, à la fin du XVe siècle, Luca Pacioli reprend cette dimension en mettant en avant son côté divin. Il traite le nombre d’or pour la première fois de façon inédite. C’est également à cette époque que la suite de Fibonacci est mise en relation avec la section dorée.

Le nombre d’or : le mythe nait au XIXème siècle

C’est finalement en 1850 que le philosophe allemand Adolf Zeising parle du nombre d’or comme étant une clé dans des domaines aussi bien scientifiques qu’artistiques. Le nombre d’or perdra à partir de ce moment-là de son intérêt mathématique, mais gagnera beaucoup plus en tant que système. Bien que des doutes persistaient, il était en revanche possible d’expliquer la beauté grâce au nombre d’or.

Le nombre d’or atteint son sommet au XXème siècle

Durant tout le siècle, le nombre d’or continue d’être un objet d’étude fascinant pour les mathématiciens, les artistes et les architectes. Alors qu’il reprenait les thèses du précédent siècle, le prince roumain Matila Ghyka appliquera cette proportion aux plantes et à l’architecture avec des règles plus flexibles et plus souples.

Plus loin, il affirmera que le nombre d’or est une preuve de supériorité culturelle, sociale et ethnique sur des populations. Beaucoup suivront sa pensée et utiliseront le nombre d’or pour comparer les morphologies d’une population pour aboutir à une supériorité raciale.

Le nombre d’or du point de vue de la géométrie

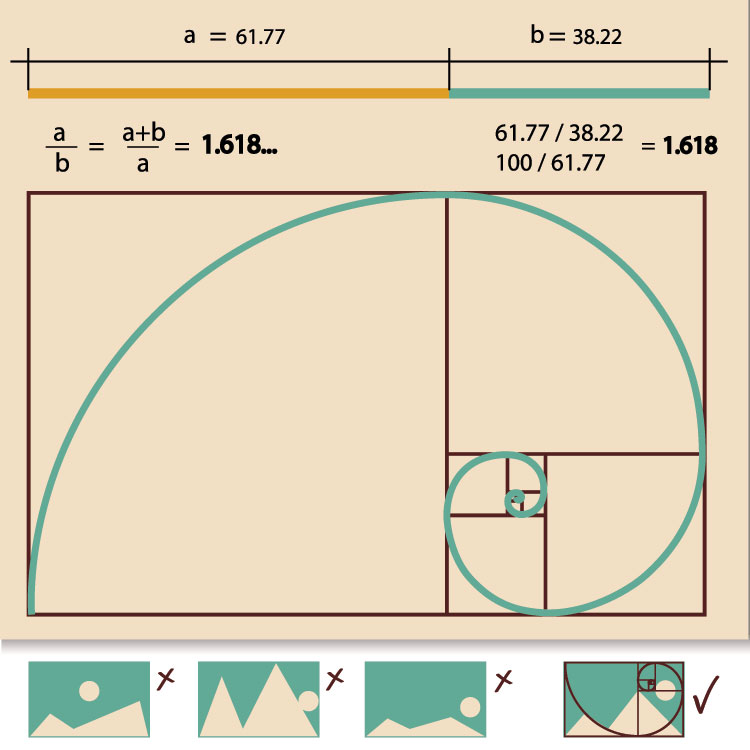
Le nombre d’or tient sa première définition de la géométrie : deux longueurs a et b respectent la proportion d’or si le rapport de a sur b est égal au rapport de a+b sur a.

A partir de ces calculs, une possibilité devient réelle : dessiner une proportion d’extrême et moyenne raison en se servant d’un compas, d’une règle ou d’une équerre. De là alors, on peut :

• Tracer un cercle C de rayon 1 ;
• Tracer à l’extrémité du rayon 1, un segment de longueur ½, perpendiculaire au rayon ;
• Tracer le cercle C de rayon ½ ;
• Tracer le segment depuis le centre du cercle C jusqu’à l’extrémité du cercle C en passant par le centre du cercle C ;
• La longueur de ce segment vaut le nombre d’or.

Il est alors possible de construire un rectangle d’or à partir de ces cercles. Le nombre d’or peut également aider à la construction de pentagones et de pentagrammes.

L' homme de Vitruve et la Joconde - Léonard de Vinci

La présence du nombre d’or dans la nature

A travers des éléments comme : les écailles d’une pomme de pin, les étamines des fleurs de tournesol, les cristaux de quartz, l’écorce d’un ananas, etc., la section dorée est omniprésente dans la nature. D’ailleurs, toute réalisation humaine imite la nature.

Dans le corps humain

La présence du nombre d'or dans le corps de l’Homme a fait également l’objet d’étude. Zeising a même essayé de mesurer le corps humain avec le nombre d’or, mais sa tentative a été abandonnée parce que les proportions du corps humain ainsi faites n’étaient pas du tout réalistes.

Le corps humain est en permanente évolution et pas forcément de manière uniforme. Toutefois, les scientifiques n’ont pas abandonné de façon définitive la recherche du nombre d’or dans le corps humain.

Elément clé de la géométrie sacrée, le nombre d'or est la base de construction de nombreux symboles de géométrie sacrée comme la fleur de vie et le cube de Métatron. S'il ne nous a pas encore livré tous ses secrets, il reste aujourd'hui plus que jamais un symbole d'harmonie et de perfection.